Whitening a matrix is a useful preprocessing step in data analysis. The goal is to transform matrix X into matrix Y such that Y has identity covariance matrix. This is straightforward enough, but in case you are too lazy to write such a function here’s how you can do it in Matlab:
function [X] = whiten(X,fudgefactor) X = bsxfun(@minus, X, mean(X)); A = X'*X; [V,D] = eig(A); X = X*V*diag(1./(diag(D)+fudgefactor).^(1/2))*V'; end
You can read about bsxfun here if you are unfamiliar with this function. Because the results of whitening can be noisy, a fudge factor is used so that eigenvectors associated with small eigenvalues do not get overamplified. Thus the whitening is only approximate. Here’s an image patch whitened this way:
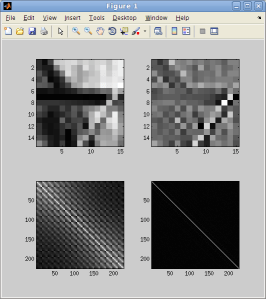
This accentuates high frequencies in the image. At the bottom you can see the covariance matrix of the set of natural image patches before and after whitening.
Here’s an explanation for why this works as well as a reference you may cite.
What about in Python? ali_m very nicely translated my code to Python on StackOverflow, which I’m reprinting here for your ease of use:
import numpy as np def whiten(X,fudge=1E-18): # the matrix X should be observations-by-components # get the covariance matrix Xcov = np.dot(X.T,X) # eigenvalue decomposition of the covariance matrix d, V = np.linalg.eigh(Xcov) # a fudge factor can be used so that eigenvectors associated with # small eigenvalues do not get overamplified. D = np.diag(1. / np.sqrt(d+fudge)) # whitening matrix W = np.dot(np.dot(V, D), V.T) # multiply by the whitening matrix X_white = np.dot(X, W) return X_white, W
8 responses to “Whiten a matrix: Matlab & Python code”
Thank you very much!
I have a question. I’m using python and when i do the “diag(1./(diag(D)+fudgefactor).^(1/2))” the resultant array of that specific computation contains complex numbers, so i get an error when i try to multiply by X*V…*V’ (the rest of the equation). I don’t understand why you don’t get the same error? Thank you very much!
Hi, Thanks for the nice description.
I am not sure, but I think there is a problem in the above code. To compute covariance matrix you are using X’ * X, so my understanding is that you are considering each row as a sample and columns are features or variable. So, for the mean removal, based on the covariance definition, we need to remove mean from each sample and put samples around the origin in the feature space. As I know, mean(X) without dimension definition and in defaults calculate means of columns. So, in the above code instead of mean removal from rows/samples we are removing means from columns. To wrap up, I think it has to be, mean(X,2) or it has to be X*X’.
Reblogged this on robot boy.
Hi
How did you calculate the covariance matrixon the left bottom corner?
Thanks
[…] Previously, I showed how to whiten a matrix in Matlab. This involves finding the inverse square root of the covariance matrix of a set of observations, which is prohibitively expensive when the observations are high-dimensional – for instance, high-resolution natural images. […]
Thanks for the snippet. But what would be a good value for fudgefactor? 0-1 or higher?
Something like 1e-6 times the largest eigenvalue of the A matrix.
[…] directly on a design matrix X where you would use the eigenvalue decomposition on X’X; whitening images is one application of this. It’s an important tool to add to your belt. Eco World Content From Across The Internet. […]